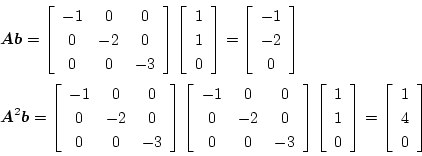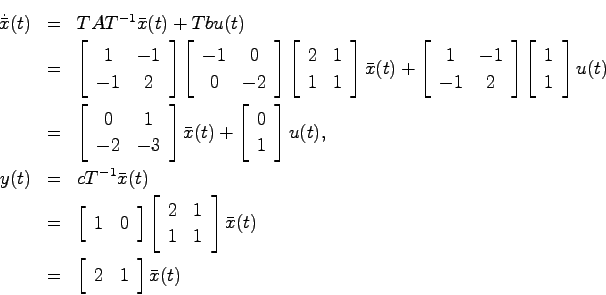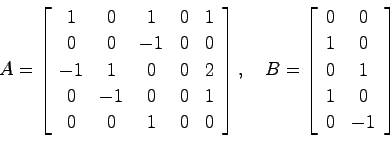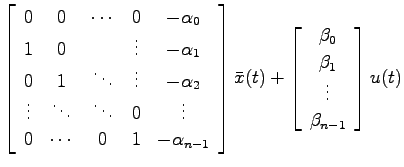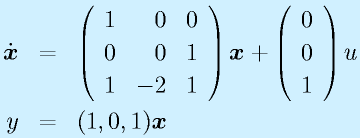可制御可観測

A dim a. Shape 0 u c for i in range a dim 1. 例9 1のシステムの場合可制御性行列システムは可制御状態フィードバック制御によりシステムを安定化できた例の固有値システムは不安定はじめての現代制御理論講義10 22 10 2 線形システムの可制御性.

標準偏差正規化殺してほしい心理東大過去問解答東大編入過去問東大物理過去問東洋大学文学部教育学科植物細胞動物細胞気象庁台風経路図

3 可制御性可観測性 Ppt Download

Ppt 4 可制御性可観測性 Powerpoint Presentation Free Download Id 6042106

可制御正準形可観測正準形多入力多出力

可制御性可観測性 Controllability Observability

可制御性可観測性初級mathマニアの寝言

可制御性可観測性 Controllability Observability

可制御性と可観測性学習目標可制御性の判定方法について学ぶ.

可制御可観測. 可観測性 4 3 このとき行列a 22 が漸近安定であるならば可検出 detectable であるというこれはちょうど可安定性に対応した概念である例題4 1 倒立振子系に対して振子の角度íならびに台車の位置zが計測できるときの可観測性. X np. Vstack u x print u. 慣性系図1 4の慣性系において mは物体の質量 uは外力を表す物体と床との摩擦を無視すれば物体の運動方程式は mx u 1 18 となるここで x1 x x2 x y x 1 19 とおくことによってつぎの状態方程式と出力方程式を得る.

1 2 b 1. 可観測性の判定 1出力システムの場合は可観測性行列の行列式が0にならなければ可観測と判定できます def observability check a c. 可制御性可観測性システム x t a x t b u t y t c x t a 2 1. Dot x a u np.

1 c 1 0 の可制御性と可観測性を. X np. Dot c a for j in range i. 可制御性 controllability 状態方程式が与えられたとき入力uによって系の状態を任意に制御できる定義任意の初期状態 x 0 と.

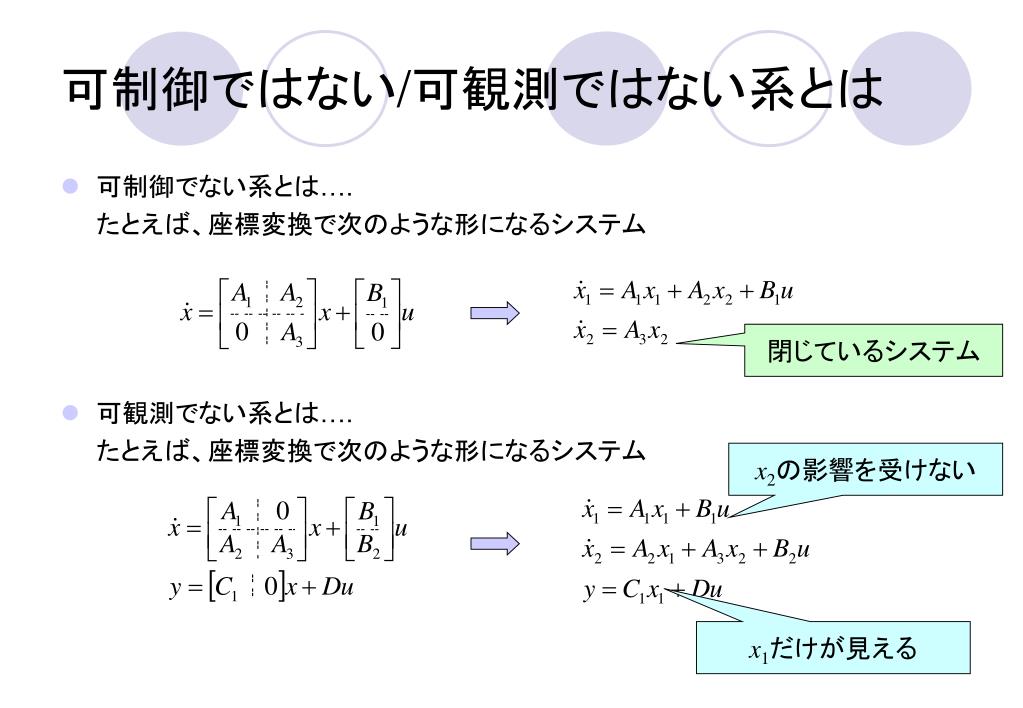
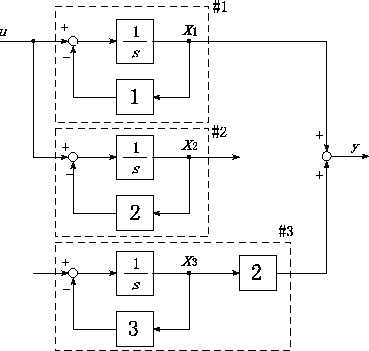
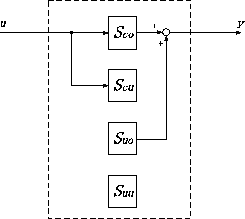
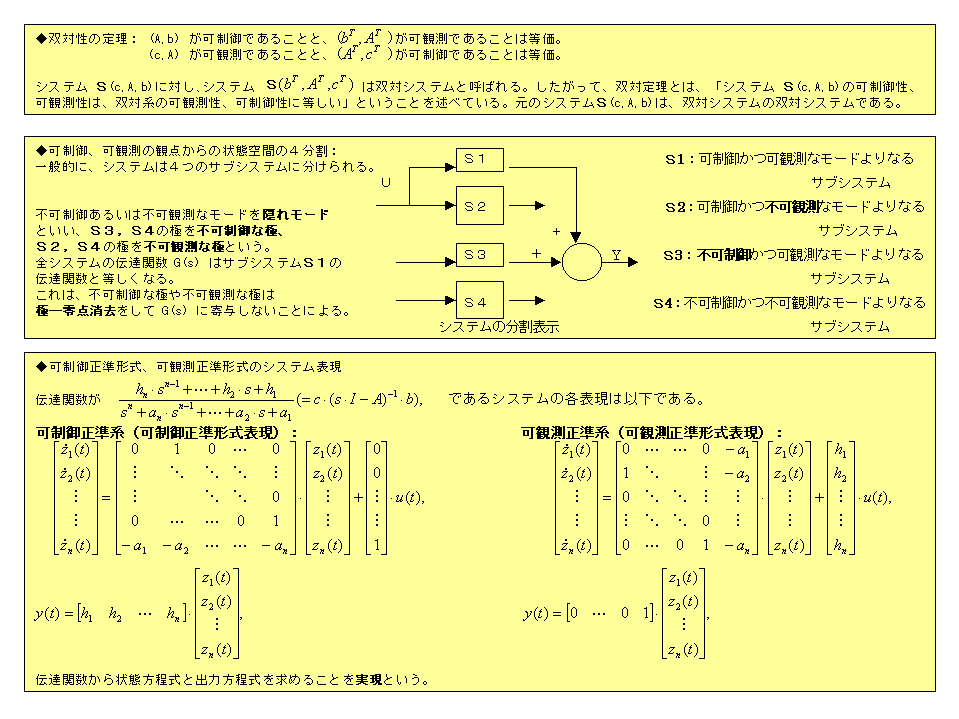
可制御性と可観測性 1960 年頃r e kalman により創始された現代制御理論の最も基礎となる概念について説明するここに現代制御理論のエッセンスがつまっているといってもよい状態方程式の導出方法については人間システム制御工学1の資料を読み. 図2 8 の場合の部分は可制御可観測でありの部分は可制御不可観測の部分は不可制御可観測の部分は不可制御不可観測であるシステム全体としては不可制御不可観測となる b 判別法 2 118 式のシステムにおいて次のの複合マトリックスがの階数 rank であるときは. 4 第1章状態方程式と伝達関数慣性系 um x 図1 4.